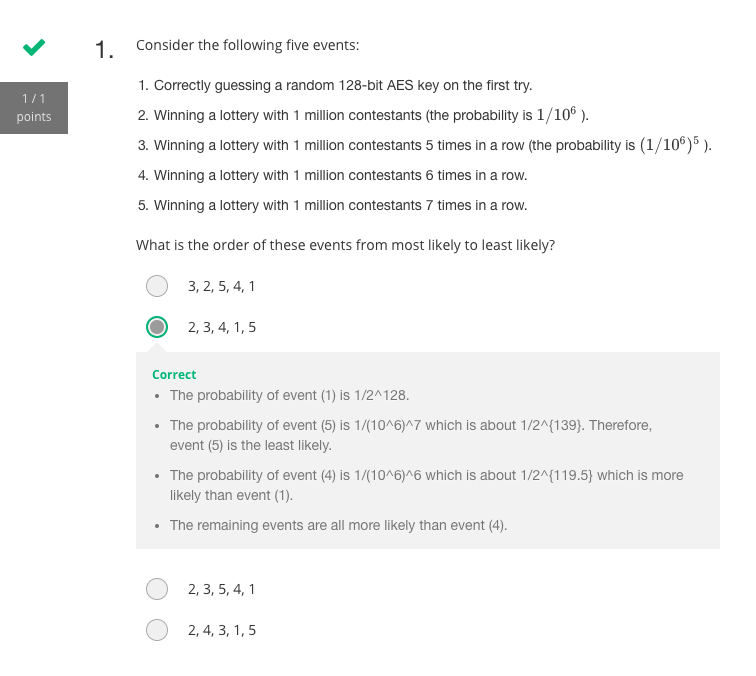
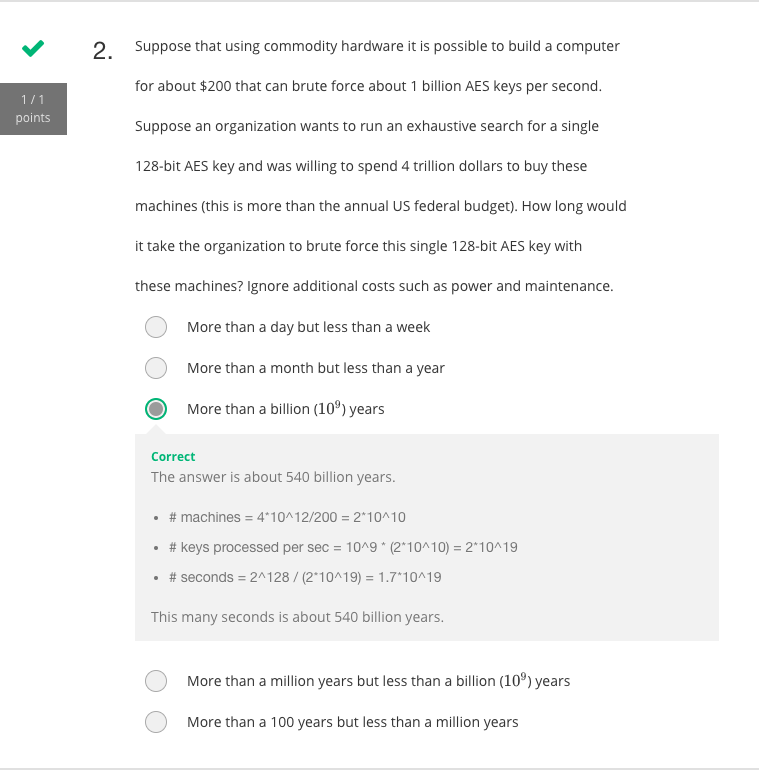
$2^{128}\approx3.4e+38$
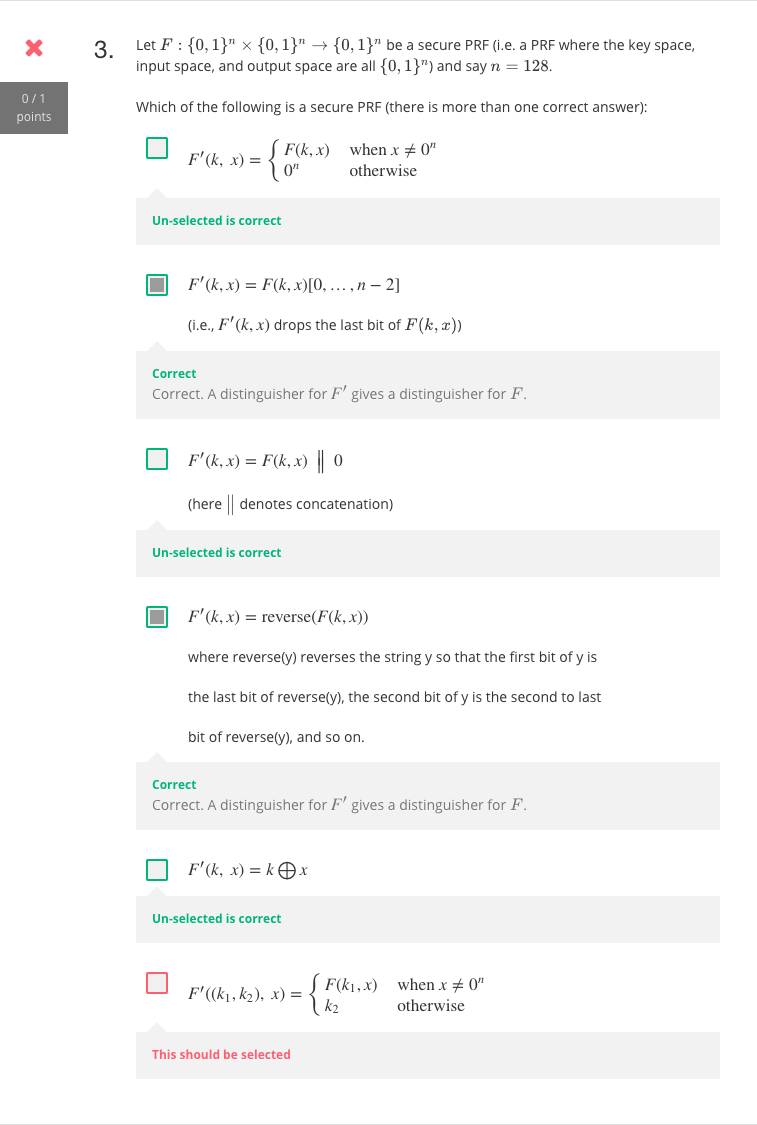
$$
\begin{align*}
m = 0^{64}:& \\
&L_1 = 0^{32} R_1 \\
&R_1 = 0^{32} \oplus F(k_1, 0^{32}) \\
&L_2 = 0^{32} \oplus F(k_1, 0^{32}) \\
&R_2 = 0^{32} \oplus F(k_2, 0^{32}\oplus F(k_1,0^{32})) \\
m = 1^{32}0^{32}:& \\
&L_1 = 0^{32} R_1 \\
&R_1 = 1^{32} \oplus F(k_1, 0^{32}) \\
&L_2 = 1^{32} \oplus F(k_1, 0^{32}) \\
&R_2 = 0^{32} \oplus F(k_2, 1^{32}\oplus F(k_1,0^{32})) \\
\end{align*}
$$
Therefore:
$$
\underset{m = 0^{64}}{L_2} \oplus \underset{m = 1^{32}0^{32}}{L_2} \equiv 1^{32}
$$
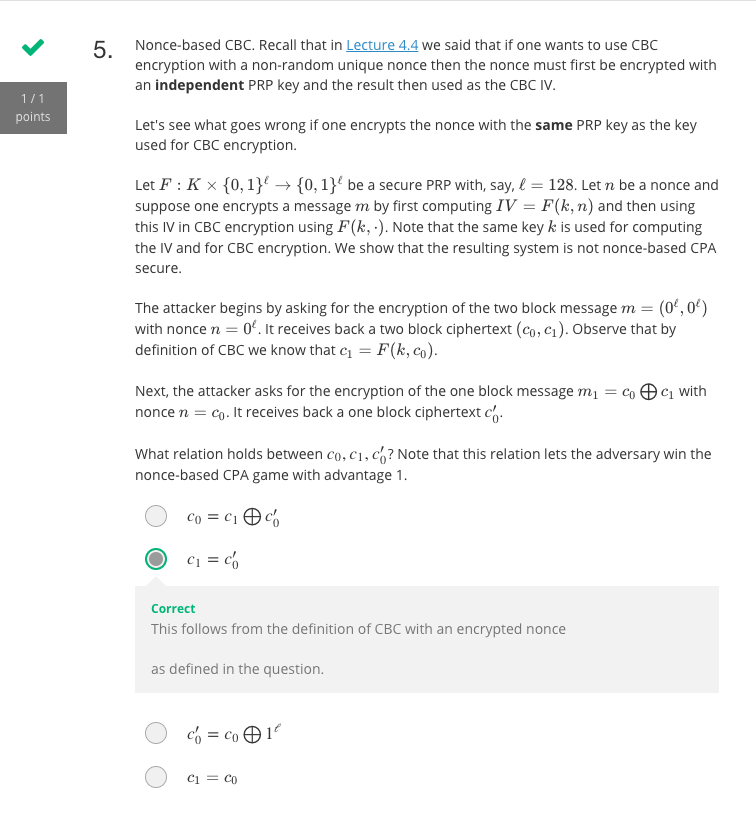$$
\begin{align*}
c' &= F(k, IV \oplus m_1) \\
&= F(k, F(k, c_0) \oplus c_0 \oplus c_0) \\
&= F(k, F(k, c_0) \oplus c_0 \oplus F(k, c_0)) \\
&= F(k, c_0)
\end{align*}
$$
Therefore:
$$
c_1 = c'_0
$$
